1. 引言

　电力的有效利用指标之一是”功率因数”。
我们之前在过去的文章中已经解释过功率因数，但是这次我想更详细地解释一下，特别是对于电路初学者
和理科学生。

2. 功率因数

　功率因数（Power Factor，PF）是指从电源提供的电力中，可以有效利用的程度。
如果所有提供的电力都被利用，则功率因数为1；如果没有被利用，则功率因数为0。
当电源电压和电流为正弦波，电路负载仅由电阻成分组成时，功率因数为1。但是，如果负载包含电容器或
电感器等电抗成分，则电源电压和电流之间会出现相位差，功率因数将小于1。
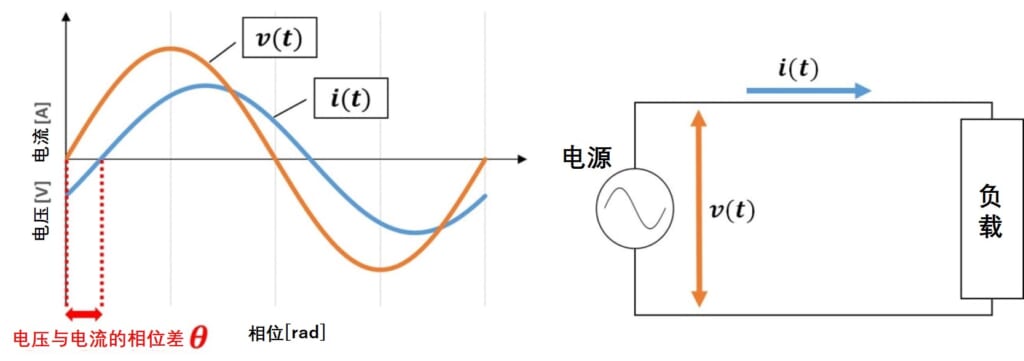
例如，我们在过去的文章中解释过，如果负载的电抗成分导致电源电压和电流之间产生相位差θ，则功率因
数由cosθ表示。

那么，让我们从功率因数的定义式推导出为什么当存在相位差θ时，功率因数会成为cosθ。
对于任意波形，功率因数可以定义为电源电压v(t)、电流i(t)，并且电源电压的周期为T，则其定义如下所示：

当电源电压为v(t) = sinωt，电压和电流之间的相位差为θ时，流经电路的电流将为i(t) = sin(ωt-θ)。
将电源电压和相位差θ代入公式（1）中计算，

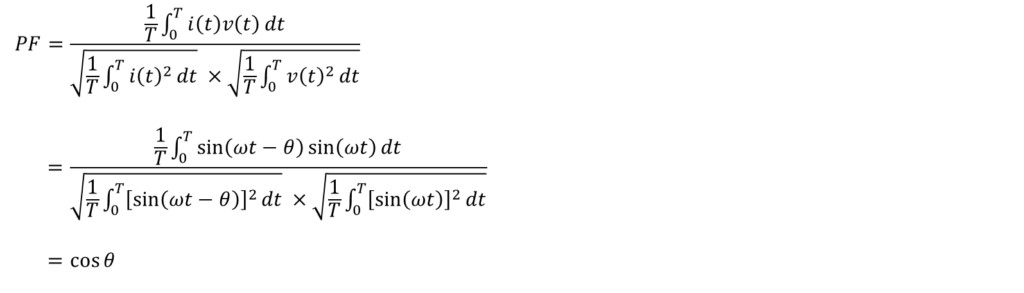
由上可得，

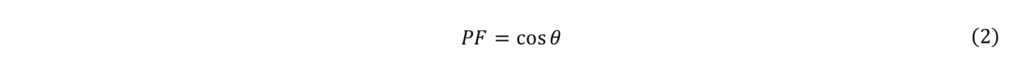
3. 任意波形的功率因数

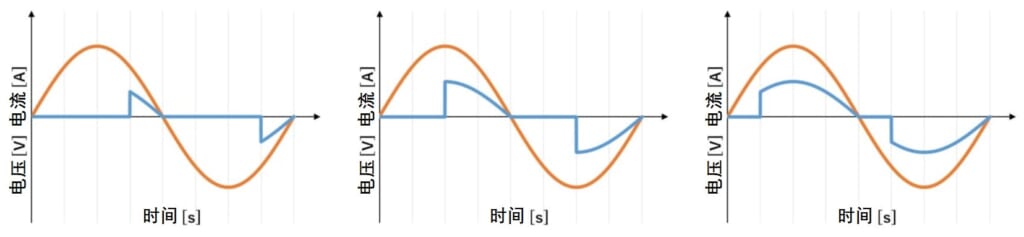
　在前一章中，我们考虑了电压和电流之间存在相位差的情况，但即使没有相位差，如果电流不是正弦波，功率因数也会降低。

例如，对正弦波电源电压进行相位控制时，电流将变为非正弦波，如图2所示。
在这种情况下，功率因数会如何？
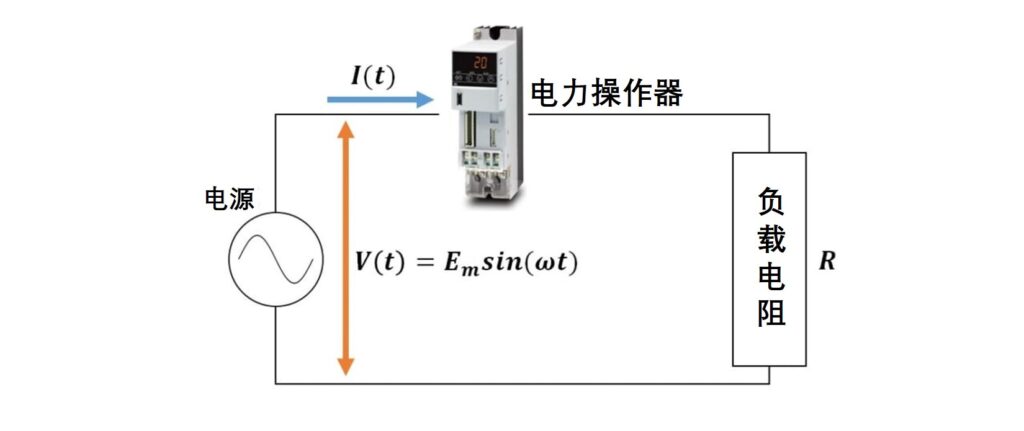
在本章中，我们将以图2中电力调节器进行相位控制时的波形为例，展示任意波形功率因数的推导过程。

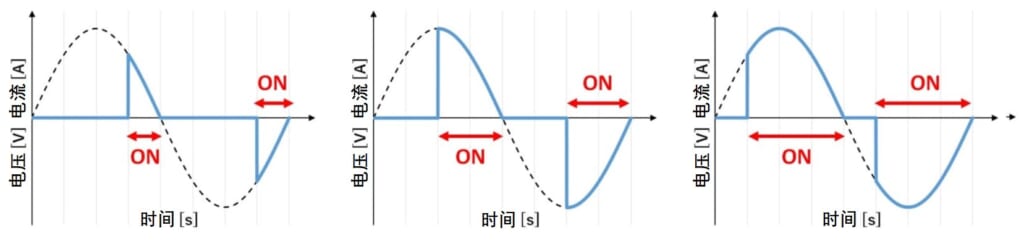
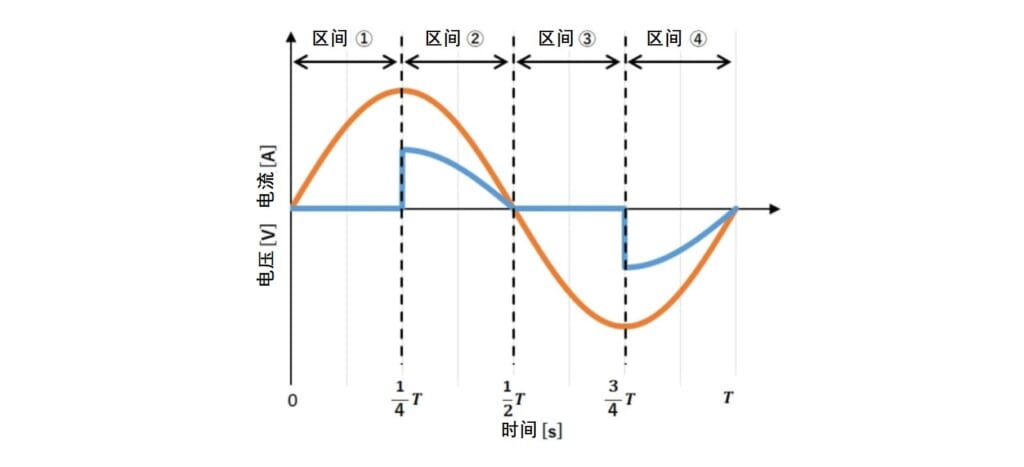
如图3所示，在相位控制中，通过改变每个电源电压周期内的ON时间比例来控制输出电力。

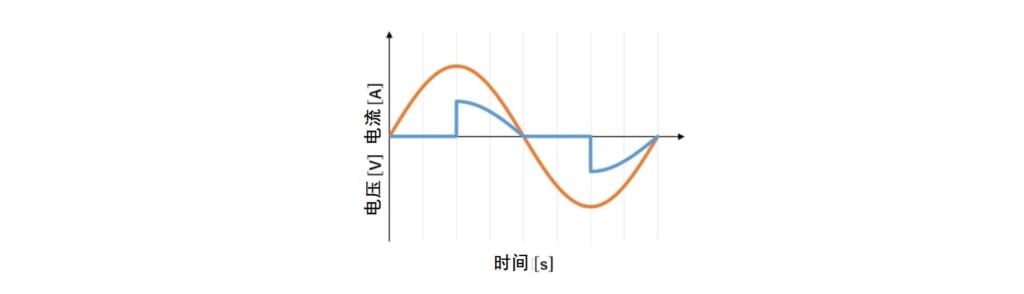
ON时间为50%控制的相位控制波形作为例子，我们来计算功率因数。为了简单起见，假设电路的电抗分量为0，电流波形如图4所示。

考虑到如图5所示的电路，并将电源电压的振幅表示为Em，电路的负载电阻表示为R，则电源电压V(t)可表示为

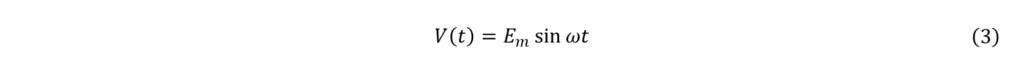
电流I(t)被分成了流动和不流动的4个区间，并可以表示为:

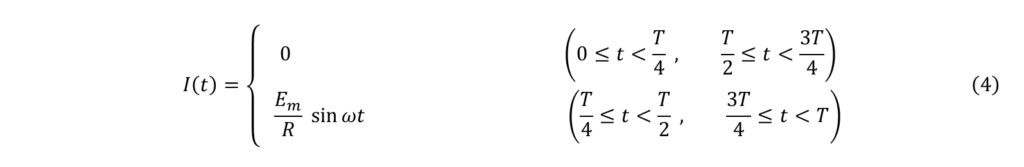
为了求解功率因数，需要计算电源电压的有效值VRMS、电流的有效值IRMS以及有功功率P。
首先，计算电源电压的有效值VRMS。根据定义式(1)，电源电压的有效值VRMS可以表示为:

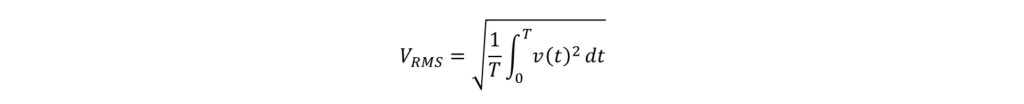
将此式代入式（3）后，

由上可得，

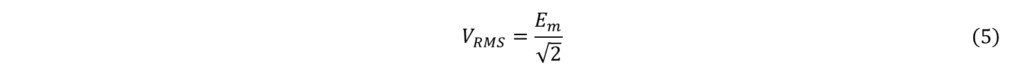
同样，我们来计算电流的有效值IRMS。 由于电流根据式(4)分为4个区间，因此我们需要对每个区间进行积分。

由定义式(1)，得到电流有效值为

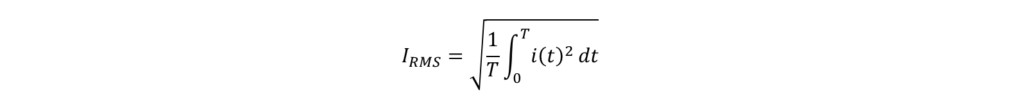
将此式代入式（4）后，

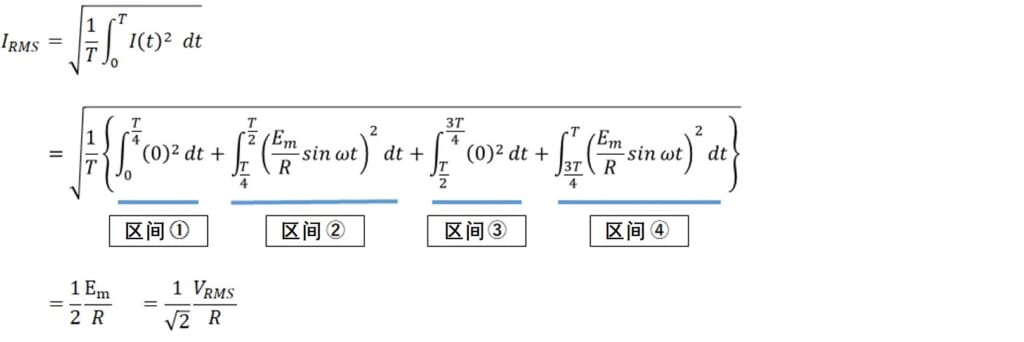
由上可得，

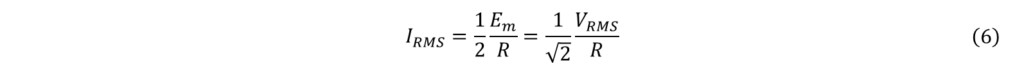
接下来求有功功率P。由定义是(1)，得到有功功率

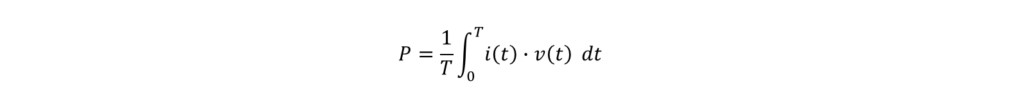
同样，我们将电流波形i(t)分成4个区间进行计算，就像我们计算电流的有效值时一样。
将这个方程中的(3)和(4)式代入，

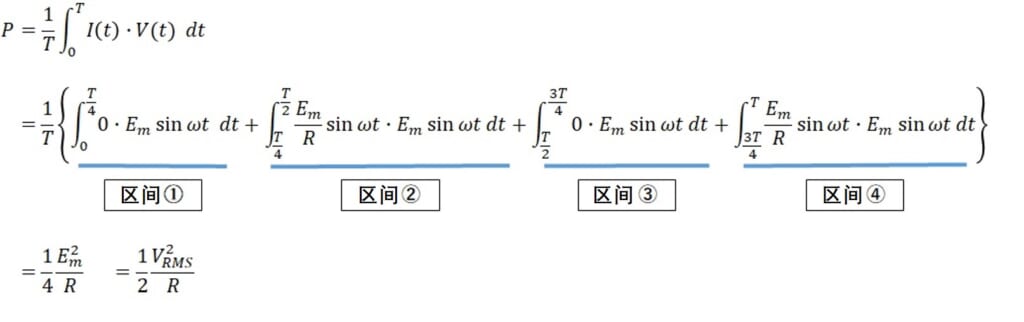
由上可得，

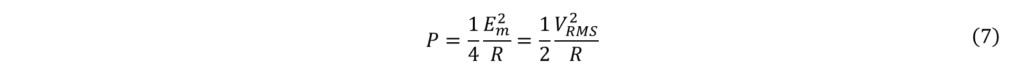
由(5),(6),(7)求得功率因数PF为，

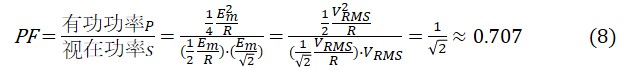
由此可见，我们已经计算出了50%占空比时的功率因数。
根据这个结果，我们可以知道，在50%占空比时，当从电源供应100W电力时，负载消耗的电力为70.7W。
相反，如果要将100W的电力加到负载上，则需要按照(9)式计算，需要提供141.4W的电力。

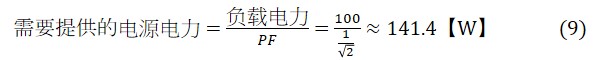
4. 总结

　本文中，我们通过计算位相控制波形的功率因数来确认任意波形有多少能有效利用电力。
非正弦波电流波形中包含谐波。如果电流中包含与电源电压不同的频率成分，即使没有相位差，功率
因数也会降低。
本文计算得到的功率因数PF被称为“综合功率因数”，其中包含了谐波和相位差导致的功率因数降低。
另外，虽然在导出示例中为了简单起见考虑了没有负载电抗成分的情况，但是如果知道电源电压和电流波形，就可以使用相同的计算方法计算所有情况下的功率因数。