技術解説
熱の基礎知識
1.熱と温度
「温度が高い」という意味で、「熱を持っている」という言葉を使っているのを耳にすることがあります。この表現は間違いではありませんが、熱と温度の間には密接な関係があるために、しばしば混同されることもあります。そもそも熱や温度とは何なのでしょうか。
熱は、電気エネルギーや力学的エネルギー、化学エネルギー、電磁波エネルギーなどとともに挙げられるエネルギーのひとつです。一方温度は、ある物体が持っている熱エネルギーの程度を表す状態量のひとつです。
ある物体の温度を測定したらT[K]だったとき、この物体が持つ熱エネルギーQ[J]は、次のような式で表すことができます。
Q=mcT ただし、m:物体の質量[kg] c:物体の比熱[kJ/kgK]
また、ある物体の温度を⊿T[K]だけ上げたい時に必要な熱量⊿Q[J]は、⊿Q=mc⊿Tとなります。
冒頭の表現を関係式の記号を使って表現すると、次のようになります。
温度が高い → Tの値が大きい
熱を持っている → Qの値が大きい
mcが定数であれば、TとQは比例関係にあるので 「Tが大きい⇔Qが大きい」 となり、冒頭の表現に問題はありませんが、材質や体積の違う2つの物体を比較するときには注意が必要です。
例えば、温度が300[K](約27[℃])の1[kg]と0.5[kg]のアルミブロックがあったとき、各ブロックが持っている熱エネルギーQ1、Q2は、
Q1=1[kg]×0.905[kJ/kg・K]×300[K]=271.5[kJ]
Q2=0.5[kg]×0.905[kJ/kg・K]×300[K]=135.75[kJ]
質量以外の条件は同じですから当然 Q1=2×Q2 となります。
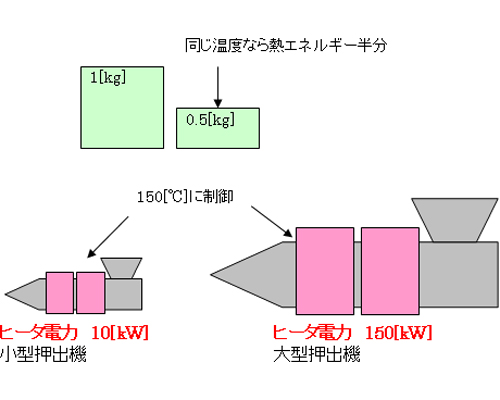
このとき、1[kg]のブロックは、0.5[kg]のブロックの2倍の「熱を持って」いますが、温度は同じです。これは、同じ温度に制御する熱処理装置でも、その規模によってヒータの電力が違うことと一致します。
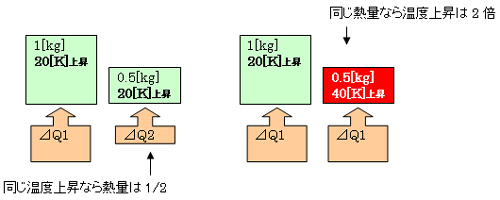
次に、加える熱量と温度上昇 ⊿Q・⊿Tを考えます。1[kg]のブロックの温度を20[K]上昇させるために必要な熱量⊿Q1、⊿Q2は、前述と同様に
⊿Q1=1[kg]×0.905[kJ/kg・K]×20[K]=18.1 [kJ]
⊿Q2=0.5[kg]×0.905[kJ/kg・K]×20[K]=9.05 [kJ]
⊿Q1=2×⊿Q2 です。
ここで、⊿Q1を0.5[kg]のブロックに加えたときの温度上昇⊿T2を計算してみましょう。
⊿Q1=18.1[kJ]=0.5[kg]×0.905[kJ/kg・K]×⊿T2[K]
⊿T2=40[K]
このように、同じ熱量に対して体積(質量)を半分にすると、その温度上昇が2倍に高くなってしまいます。
2.比熱と熱容量
比熱: 温度の変化のしにくさを示す値。単位質量の物質の温度を1[K]上げるために必要な熱量。
物質固有の物性値で、物体の形状・体積などによらない。
熱容量: 比熱と同様に、温度の変化のしにくさを示す値で、比熱に物体の質量をかけたもの。
物体の温度を1[K]上げるために必要な熱量。
前出の式 Q=mcT において、比熱がcでしたので、このとき、熱容量をCとすると C=mcとなります。
従って、熱容量の式にすると、 Q=CT と表せます。
では、比熱も熱容量も、温度変化のしにくさを表しているのなら、どちらの言葉を使っても問題なさそうですね! と言いたいところですが、実際は、問題ありなのです。
今、下図のように0.03[m^3](1×1×0.03 [m])のアルミプレートとステンレスプレートがあった場合、それぞれの比熱と密度から、熱容量を求めることができます。
※体積0.03[m^3]とする。
| アルミ | ステンレス | |
| 比熱 [kJ/kg・K] | 0.905 | 0.46 |
| 密度 [kg/m^3] | 2688 | 7800 |
| 熱容量 [kJ/K] ※ | 72.98 | 107.64 |
ここで比熱と熱容量の値を材質で比較してみると、
比熱: アルミ > ステンレス
熱容量: アルミ < ステンレス
となっているのがわかります。
比熱も熱容量も温度変動のしにくさを示しているはずですが、逆の結果を示しています。どちらの方が、温度変動しにくいのでしょうか?
正解は、「ステンレスの方が変動しにくい」です。
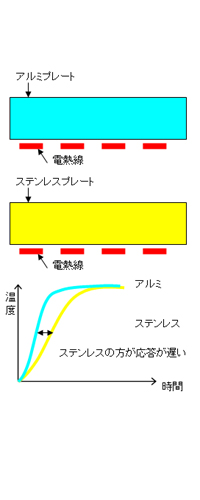
同じヒータ電力で加熱したときのそれぞれのプレート上表面温度変動は右のグラフに示すようになります。
この値の食い違いは、比熱が単位質量あたりの物性値であり、熱容量には質量を含むところがポイントになっています。
プレートヒータの比較のように、体積(形状)を決めて材質の違いによる特性を比較する場合には質量が等しくならないので、熱容量のように、各物体ごとに決まる値か、あるいは単位体積あたりの物性値を比較すればよいのです。
今、単位体積あたりの物性値を仮に「単位体積あたりの熱容量」をAとすると、
A=比熱×密度[kJ/m^3・K] となるので、
A(アルミ)=2432.64
A(ステンレス)=3588
比熱: アルミ > ステンレス
熱容量: アルミ < ステンレス
A: アルミ < ステンレス
したがって、同じ形状の2つのプレートの、温度変動のしにくさを表現するのに比熱は適していません。
「ステンレスのほうが熱容量が大きいので、温度変化が遅い」
あるいは、
「ステンレスのほうが単位体積あたりの熱容量が大きいので、温度変化が遅い」となります。
では最後に、プレートの熱容量の大小が、実際のヒータを制御する場合にはどんな影響を及ぼすかを考えてみましょう。
普通、熱容量の大きいプレートでは、設定温度に到達するまでに時間がかかるか、大電力が必要になりますが、突発的な温度変動も少ないため、外乱に強いのが特徴です。
また、制御出力に対する応答の遅れが大きいため、PID定数のゲインを高く設定するとオーバーシュートが大きくなったり、安定性が損なわれる危険性があります。このため、熱容量の大きい制御対象にオートチューニングをかけると低いゲインが算出されます。
一方、熱容量の小さいプレートでは、制御出力に対する応答が速いので、オートチューニングをかけると、高いゲインが算出されます。また、わずかな外乱にも温度変動の影響を受けやすいため、高速な制御が必要となります。
このような制御対象には高速サンプリングの温度調節計や、位相制御・ゼロクロス制御ができる電力操作器の使用が有効です。
