私たちの身の回りには、携帯電話やパソコン、テレビなど、電波を利用した様々な無線機器があふれています。
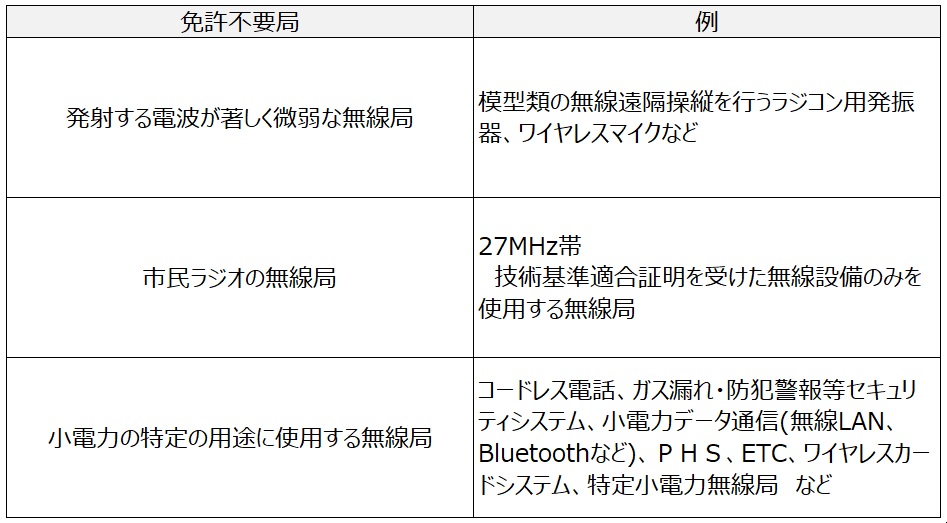
無線機器は通信用配線が不要で機器の設置場所の自由度が高いことから、遠隔・移動体などを中心に産業界でも使用されることが多くなっています。その中でも“免許不要局”に分類される無線機器は、免許・資格不要で誰でも使用できることから広く普及しています。
理化工業で展開している免許不要局無線機器としては無線温度センサ変換器 NWSシリーズがあります。離れたところに設置した温度センサのデータを無線で取得できるので、省配線の温度計測システムが構築できます。
無線通信に使用する電波は、周波数に依存した物理的な特徴があり、それを踏まえた運用がされています。下図は総務省HPに掲載されている周波数ごとの分類と主な用途です。
ここでは、周波数とアンテナサイズ・通信速度・通信距離の関係について簡単に解説します。

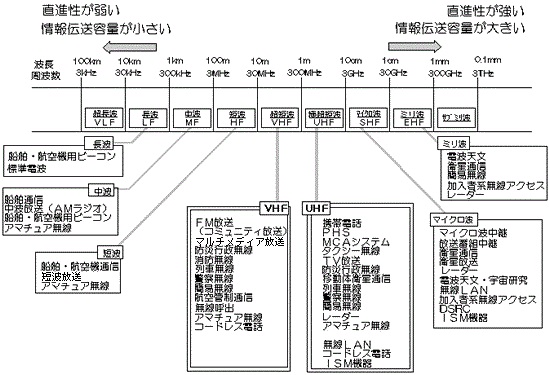
図 1　周波数ごとの主な用途と電波の特徴　（出典：総務省HP）https://www.tele.soumu.go.jp/j/adm/freq/search/myuse/summary/index.htm

表 1　免許不要局の例

1. 周波数とアンテナサイズ
無線機器はアンテナを介してデータなどの信号を送受信します。
アンテナから放射される電波は、共振させた場合に最も強くなります。共振させるためにはアンテナサイズを使用する周波数の波長に合わせる必要があります。構造がシンプルで良く使用されるスリーブアンテナの場合は、1/2波長のときに効率よく共振します。
波長λ [m]は電波の進む速度c [m/s]と周波数f [Hz]を使って次の式で表されます。

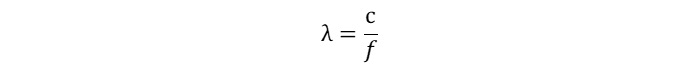
（周波数の単位[Hz]は[1/s]と置き換えられます）

したがって、周波数が高いほど、アンテナサイズを小さくできることがわかります。
電波の進む速度を30万[km/s]、周波数2.4[GHz]とした場合の波長を上式に当てはめて算出すると

となります。更に、同じ免許不要局でよく使用される周波数帯に920[MHz]がありますが、この場合のアンテナサイズを同様に求めると

となり、2.4[GHz]の場合と比べると2.6倍もの大きさになってしまいます。
下図に示したアンテナのように、アンテナとなる導体を直線状に配置するのが最もシンプルな構造ですが、アンテナサイズが無線機器のサイズを大きく左右するため、さまざまな小型アンテナが開発されています。
現在では周波数によらず無線機器の小型化が目覚ましいですが、小型アンテナは性能劣化が避けられないため、目的に応じて適切な設計が求められます。

2. 周波数と通信速度と消費電力
次に、周波数と通信速度について考えます。
無線通信ではデータを送る際、電波にデジタル信号(0と1の信号)のデータを乗せることで通信を行います。したがって、たくさんのデータを送るためには波の数が多く必要です。
周波数とは１秒間に含まれる波の数です。周波数が高くなると単位時間当たりの波の数が多くなるため、１秒間に送ることができるデータ量が多くなります。
つまり、周波数が高いほど通信速度を速くできるといえます。

表 2　周波数とデータ送信

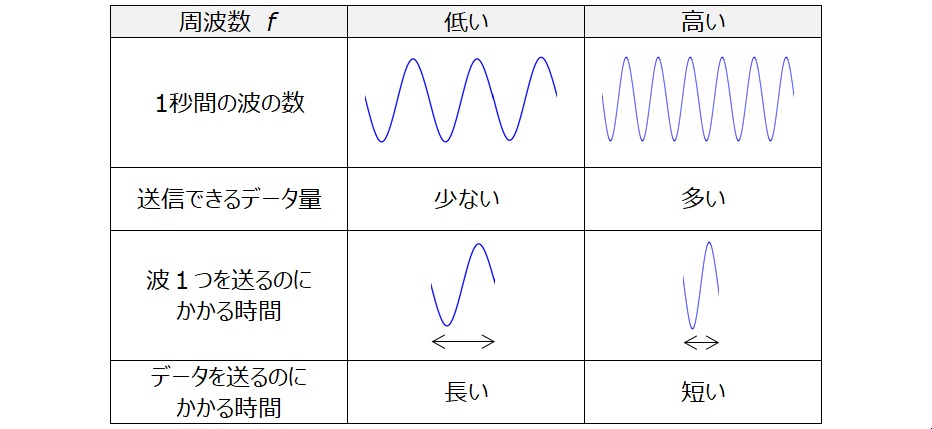
一般に、無線機器の消費電力は送受信中が最も大きくなることと、データ量が大きいほど送受信に時間がかかることから、通信速度の速い高周波数帯の無線通信には消費電力の面でもメリットがあります。
※実際の無線通信による通信速度は、通信規格や法律による制限・帯域幅の割り当て等の影響を大きく受けますが、それらを総合しても概ね周波数が高いほど通信速度を速くできるという傾向がみられます。

3. 周波数と通信距離
無線機器の性能の中でも特に関心が高いのは通信距離ではないでしょうか。しかし、信号の経路をケーブルで規定できる有線通信に比べて、公共の空間を経路に含む無線通信は、送・受信器間の経路を規定できず設置環境の影響を大きく受けます。このため、無線機器性能としての通信距離を明確にしづらいのが悩ましいところです。
送信器から出力された無線電力は様々な要因で減衰しながら受信器に到達します。受信器が検知できる下限電力になる地点までの距離が通信距離であると考えることができるので、無線電力を減衰させる要因を調べることで、通信距離に与える影響がわかります。

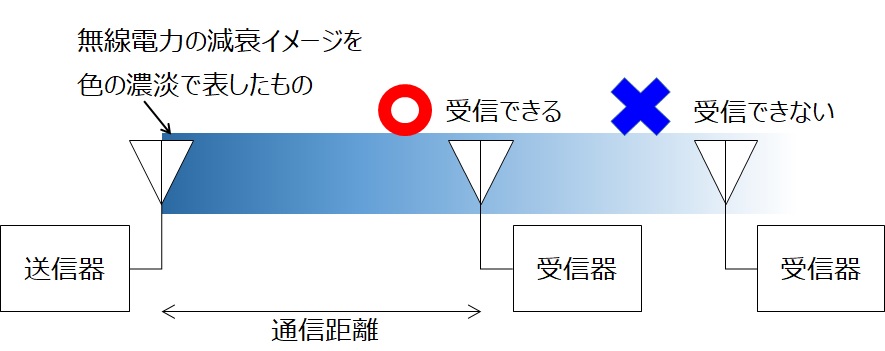
図 2　無線電力の減衰と通信距離

ここでは、無線電力を減衰させる代表的な要因について紹介します。

表 3　無線電力を減衰させる代表的な要因

このうち、自由空間損失とは、障害物のない理想的な空間における無線送信電力の損失であり、送信電力Ps と、受信電力Pr の比で得られるため、送受信アンテナ間の距離d[m]、電波の波長λ [m]を使って以下の式で表現されます。

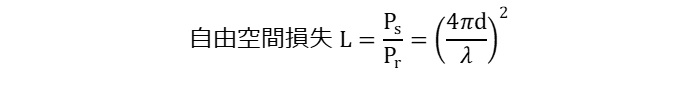
この式からは、損失が距離dの2乗に比例するということと、波長λの2乗に反比例することがわかります。波長は周波数の逆数（λ ＝c / f）であることから、自由空間損失Lは周波数の2乗に比例するため、理想的な空間であっても周波数が高いほど通信距離が短くなることがわかります。
また、障害物のサイズが波長に対して大きいほど影響を受けるため、これも周波数が高いほど損失が大きくなります。
このように、通信周波数が高いと通信距離に対しては不利ですが、設置環境やアンテナの工夫などで通信距離を延ばすことができる場合もあります。通信速度や小型化などのメリットも併せて評価し通信周波数を選択するのがよいでしょう。