技術解説
位相制御と力率 任意の負荷電流波形から力率を求めるためには?
1. はじめに
電源からの電力の有効利用を表す指標として、「力率」があります。
力率については過去の記事でも解説しましたが、今回は電気回路初学者や理系の学生の皆さん向けに、もう少し詳しく解説したいと思います。
2. 力率とは
力率(Power Factor,PF)とは、電源から供給される電力のうち、どの程度有効利用できているかを示す指標です。
供給される電力をすべて利用できているのならば1、全く利用できていないのならば0になります。
電源電圧と電流が正弦波で、回路の負荷が抵抗成分のみである場合には力率は1となりますが、コンデンサやインダクタなどのリアクタンス成分を含む場合、電源電圧と電流の位相がずれて力率が1より小さくなっていきます。
例えば、負荷のリアクタンス成分により、電源電圧と回路に流れる電流に位相差θが生した場合の力率がcosθで表されることは過去の記事で解説しました。
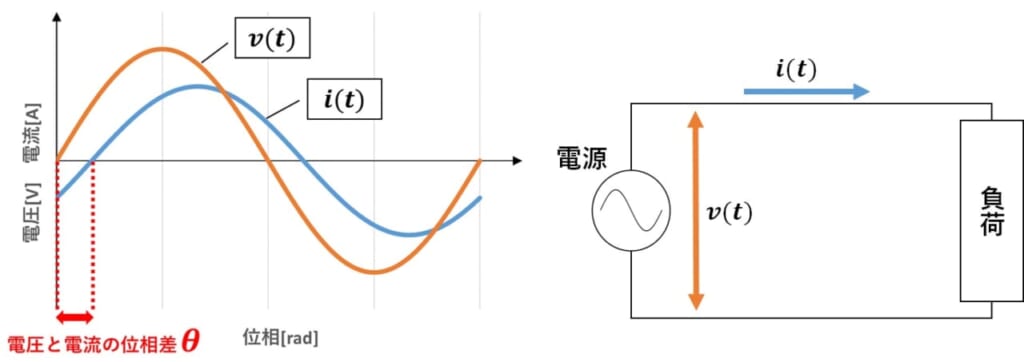
図1 電源電圧-電流の位相差θ
では、なぜ位相差θがある場合の力率がcosθになるのか、力率の定義式から導出してみましょう。
任意の波形に対する力率は、電源電圧をv(t)、電流をi(t)、電源電圧の周期をTとすると、以下の式によって定義されます。

電源電圧をv(t) = sinωt、電圧と電流の位相差をθとすると流れる電流はi(t) = sin(ωt-θ)になります。
(1)式に電源電圧と位相差θがある場合の電流を代入して計算してみると、
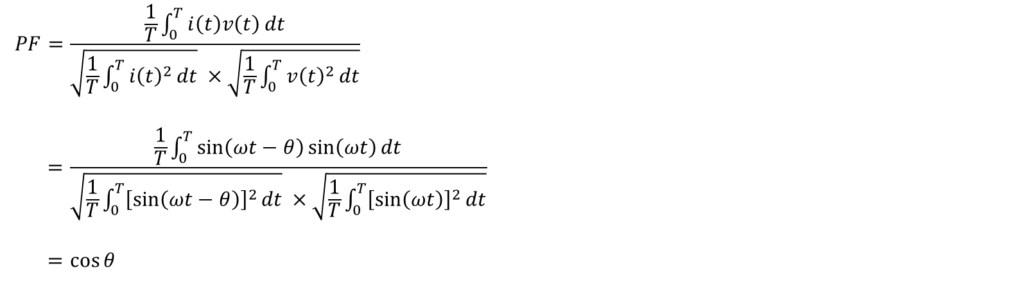
よって、
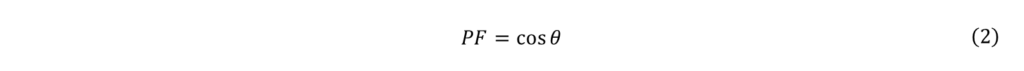
このように、電源電圧と電流が正弦波の場合、力率がcosθで表せることが分かります。
3. 任意の波形の力率
前章では電源電圧と電流に位相差がある場合を考えましたが、位相差がなくても電流が非正弦波になると力率が小さくなります。
例えば、正弦波の電源電圧に対して位相制御を行うと、電流は図2のような非正弦波になります。
この場合の力率はどうなるでしょうか。
本章では図2のように電力調整器で位相制御した時の波形を例に任意波形の力率の導出過程を示します。
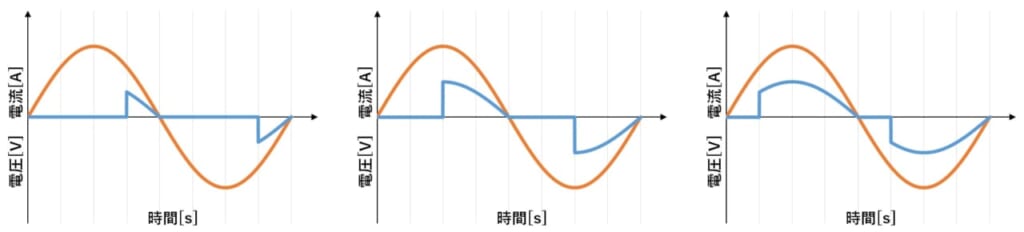
図2 位相制御をしたときの電源電圧(オレンジ)・電流(青)の例
図3のように、位相制御では電源電圧の周期毎におけるON時間の割合を変化させることで出力電力を制御しています。
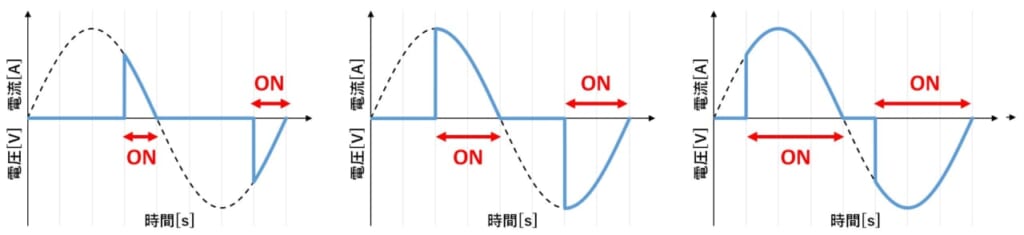
図3 位相制御でON時間を変化させた電流波形(青)とON時間100% 時の電流波形(点線)
では、ON時間50%で制御された位相制御波形を例として、力率を求めましょう。簡単のため、回路のリアクタンス成分を0とした場合、電流波形は図4のようになります。
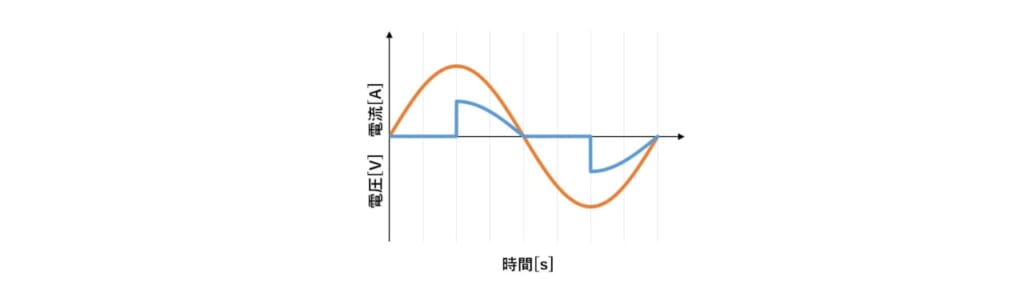
図4 ON時間50% で位相制御したときの電源電圧(オレンジ)・電流(青)
図5のような回路を考え、電源電圧の振幅をEm、回路の負荷抵抗をRとすると、電源電圧 V(t)は、
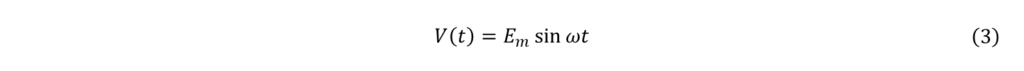
電流 I(t) は、電流の流れる区間、流れていない区間を4分割して、以下のように表されます。
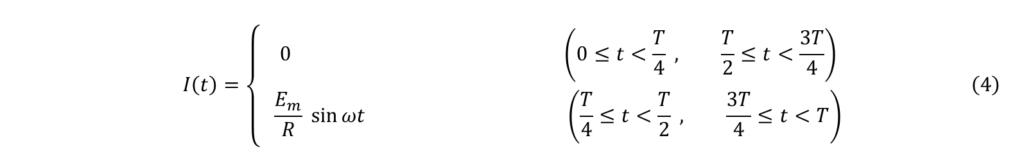
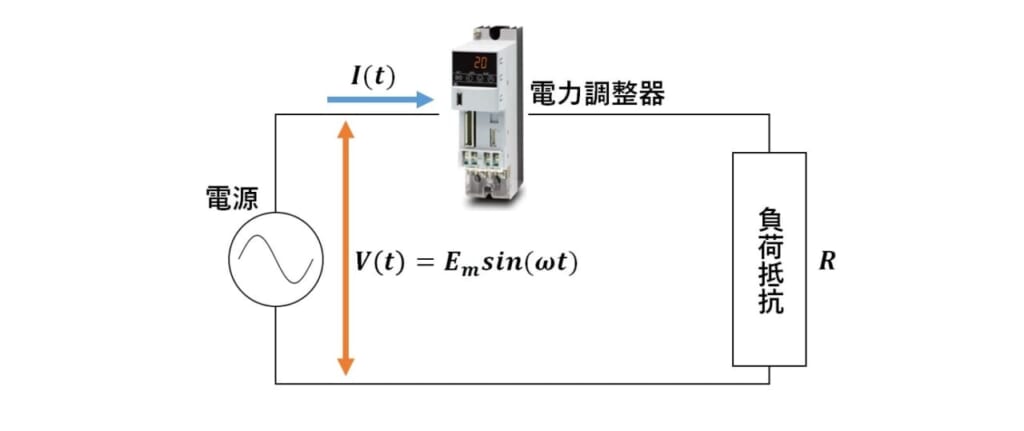
図5 位相制御の回路図
力率を求めるためには、電源電圧実効値VRMS 、電流実効値 IRMS 、有効電力Pを求める必要があります。
まず、電源電圧実効値 VRMS について求めます。定義式(1)より、電源電圧実効値 VRMS は
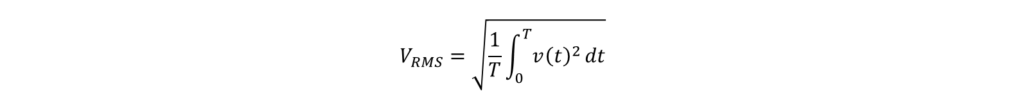
この式に(3)式を代入すると、

よって、
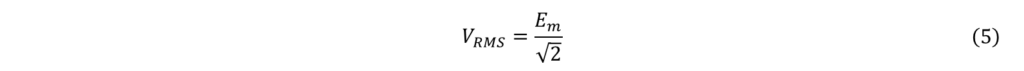
同様に電流実効値 IRMS を求めます。
電流は(4)式より、4つの区間に分割しているため、それぞれの区間に対して積分を行います。
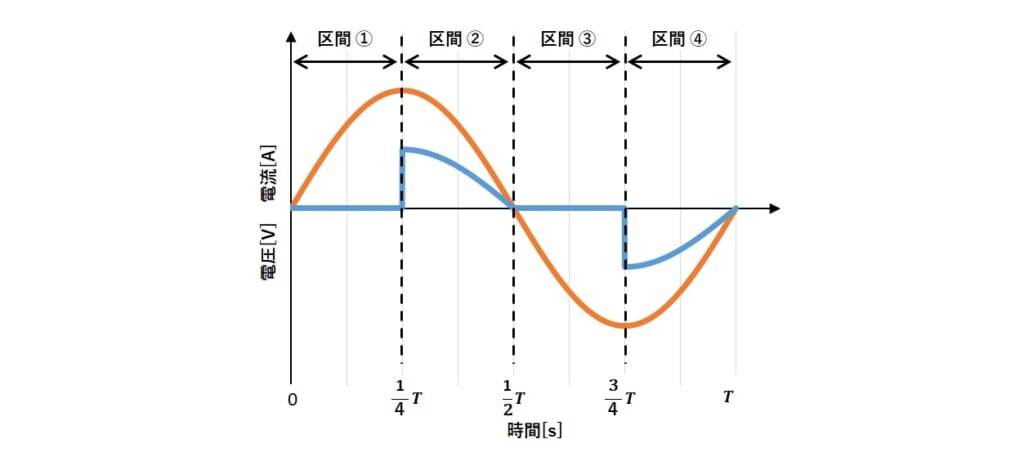
図6 電流の積分区間①~④について
定義式(1)より、電流実効値は
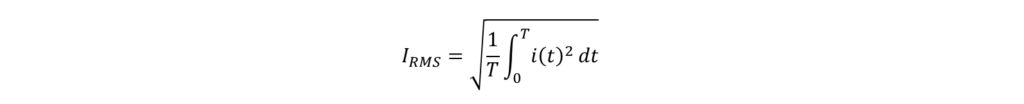
この式に(4)式を代入すると、
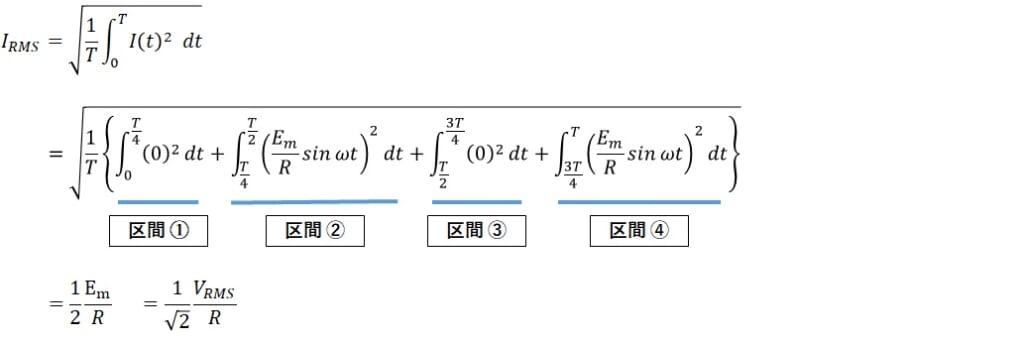
よって、
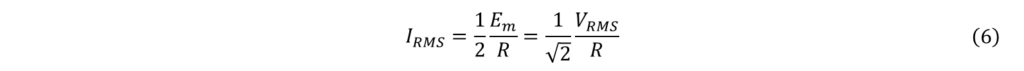
次に、有効電力Pを求めます。定義式(1)より、有効電力は
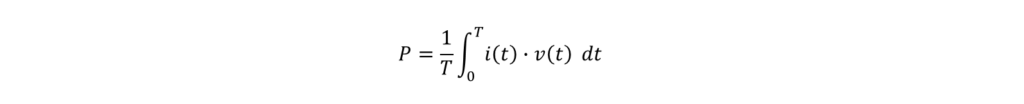
また、電流実効値を算出した時と同様に、電流波形i(t)を4区間に分けて計算します。
この式に(3)(4)式を代入すると、
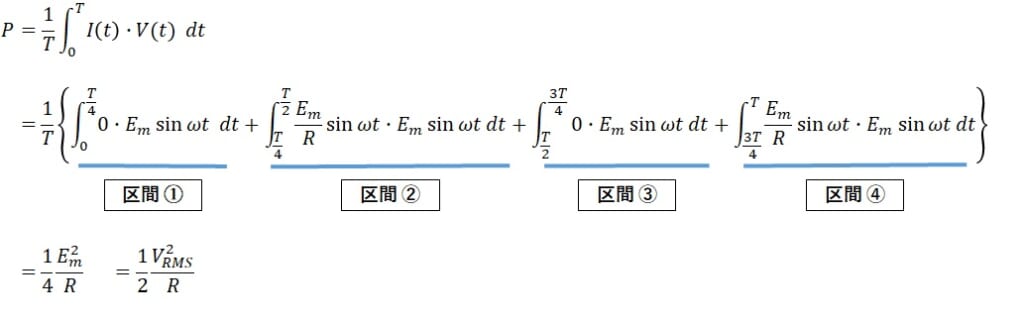
よって、
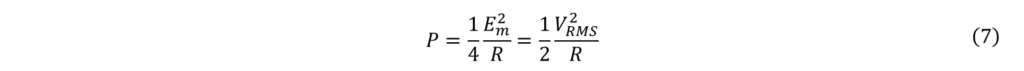
(5),(6),(7)より、力率PFを求めると、
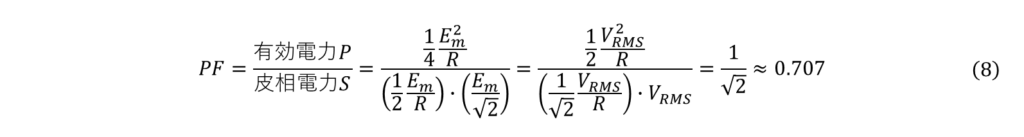
以上により、ON時間50%時の力率を求めることができました。
この結果から、ON時間50%時において、100Wの電力を電源から供給した際、負荷での消費電力は70.7Wとなることが分かります。反対に、100Wの電力を負荷に加えたい場合、(9)式のように計算して141.4Wの電力供給が必要となります。

4. まとめ
本記事では位相制御波形を例として力率を求めてみることで、任意の波形がどれほど電力を有効利用できているかを確認しました。
正弦波でない電流波形には高調波が含まれています。電源電圧と異なる周波数成分が電流に含まれている場合、位相差がなくとも力率は小さくなります。
今回求めた力率PFは”総合力率”と呼ばれるもので、高調波と位相差による力率の低下が含まれています。また、導出例では簡単のため負荷にリアクタンス成分が無い場合を考えましたが、電源電圧と電流の波形が分かっていれば、同様の計算方法ですべての場合で力率を計算することができます。
