１．センサの応答性

センサの応答性を表す方法として、最終安定温度の90%(または、95%,99%など)に到達するまでの時間を示すことが一般的です。（例えば、弊社製品のST-50は、「応答時間（95%指⽰）　0.08秒」と応答性をうたっています）
この応答時間は、いわゆる時定数と同様で、温度の変化量によらず、センサの形状や物性、加熱・放熱環境によって決まります。
温度の変化量とは、初期温度を例えば25[℃]としたときに最終温度が100[℃]であれば、変化量は75[℃]になります。最終温度が30[℃]であれば、変化量は5 [℃]です。

「最終温度が異なっても応答時間(応答性)が同じである」を言い換えると、
「75[℃]の温度上昇にかかる時間と、5[℃]の温度上昇にかかる時間が同じである。」
ということになりますが、これには違和感がある方も多いのではないでしょうか。

これは、例えばセンサを挿入した水を①一定火力で加熱し続けた場合の温度上昇と、②温度一定の水にセンサを挿入した場合のセンサ温度上昇を、混同したときに陥りやすい誤解です。
センサの応答時間は、“センサ温度が測定点と同じ温度になるまでにかかる時間“であるため、後者の温度一定の水にセンサを挿入した場合の温度上昇になります。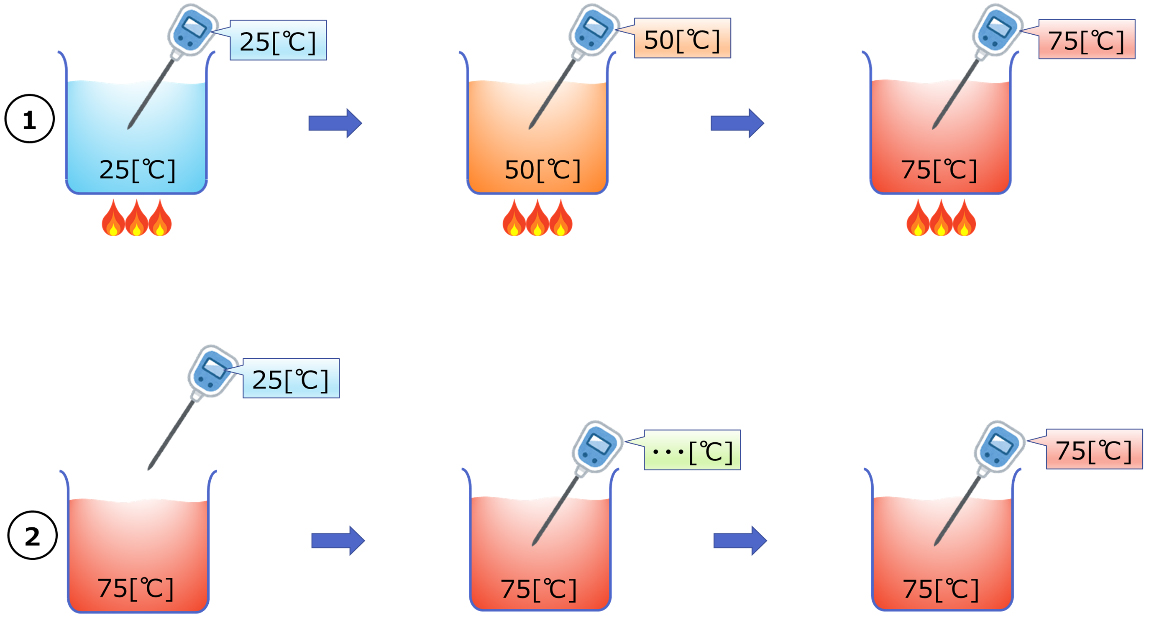

ここでは上記2つの温度上昇の違いについて解説します。

２．温度上昇のメカニズム
前述した2つの場合について、それぞれの温度上昇のメカニズムを説明します。
①センサを挿入した水を一定火力で加熱し続けた場合の温度上昇
②温度一定の水にセンサを挿入した場合のセンサ温度上昇

①センサを挿入した水を一定火力で加熱し続けた場合の温度上昇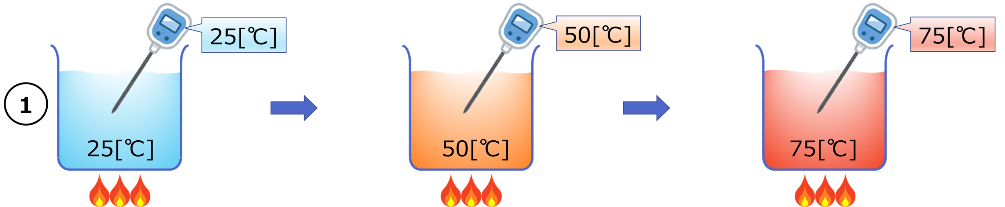

センサを挿入した25[℃]の水を一定の火力で加熱する場合を考えます。話を簡単にするため、ここでは以下の3点を仮定します。
・火力のすべてが水とセンサの温度を上昇させるために働き、外部へ熱が逃げることはない
・水は一様に加熱され、容器内に温度差・ムラは生じない
・水とセンサの温度は一致しているとみなす（温度変化時に水とセンサの温度が同一に変化する）
加熱する火力をP[W]、水の熱容量C_w[J/℃]としたとき、単位時間あたりの水の温度上昇⊿T_w[℃/s]は以下のような式で表せます。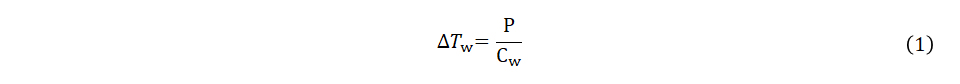

熱容量C_wは、水の比熱と質量をかけたもので、温度変化のしにくさを表します。
比熱と熱容量についての解説はこちら
⊿T_wは単位時間当たりの水の温度上昇なので、Pで加熱し続けた　t秒後の水の温度T_w(t)[℃]は、水の初期温度T_w0[℃]を用いて、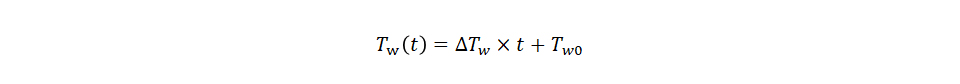
式(1)を代入して、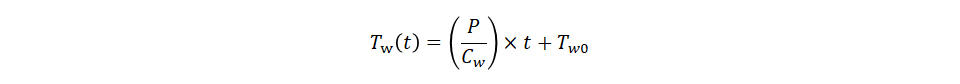

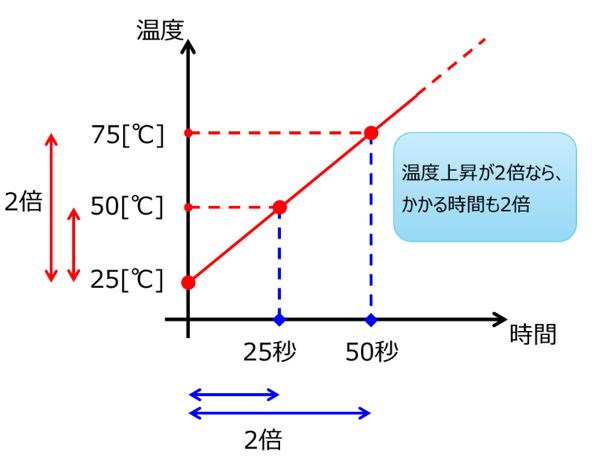
式、グラフの両方からわかるように、温度上昇と、温度上昇にかかる時間は比例関係にあるため、例えば水の温度が25[℃]上昇するのに25秒かかったとすると、50[℃]温度上昇するためには50秒かかります。これが、一定火力で加熱し続けた場合の温度上昇であり、熱容量の逆数を比例係数とした直線になります。
※実際には、周囲への放熱があるため、温度上昇は直線にはならず次第にゆるやかになります。

②温度一定の水にセンサを挿入した場合のセンサ温度上昇
次に、温度一定の水にセンサを挿入した場合を考えます。この例では、以下の点を仮定します。
・水の温度は一様かつ一定に保たれるよう制御されており、センサの挿入、時間経過によって変化しない
また、①では水の温度上昇とセンサ温度が常に一致しているとしましたが、ここでは、水によって加熱されるセンサ自身の温度上昇を考えるため、水とセンサに温度差があることがポイントです。この場合のセンサ温度の変化は、温度の高い物体から温度の低い物体へ熱が移動するという伝熱の基本法則によって説明できます。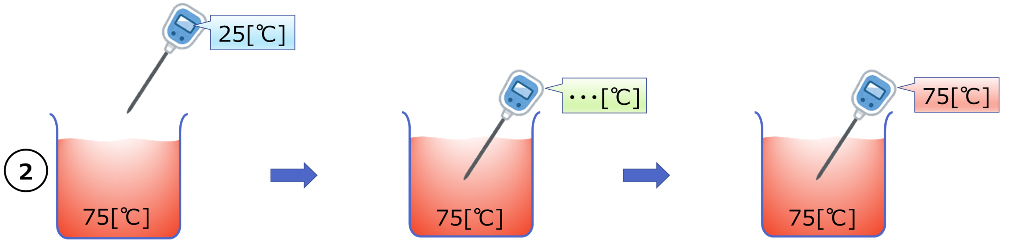

上図の水とセンサのように、温度差のある物体が接触したときの単位時間当たりの熱の移動量P_w [W]は、水の温度T_w [℃]、センサの温度T_s[℃]を用いて以下のように表すことができます。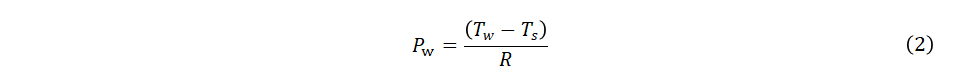

熱抵抗R[℃/W]は熱の伝わりにくさを表し、水とセンサの物性や接触条件などで決まります。
また、「単位時間当たりの熱の移動量」を、伝熱の分野では「熱流量」と言います。
この式から、熱流量P_wは水とセンサの温度差に比例することがわかります。
ここでは水の温度T_wは一定ですが、センサの温度は時々刻々と変化するため、熱流量P_wもそれに合わせ変化します。
具体的には、下の図に示すようにセンサを挿入した直後が最も温度差が大きく、熱流量も大きいですが、センサの温度が上昇するにつれ熱流量が小さくなります。そして、センサの温度が水の温度と等しくなった時(T_s=T_w)に熱の移動がなくなり(P_w=0)、それ以降センサの温度は変化せず安定します。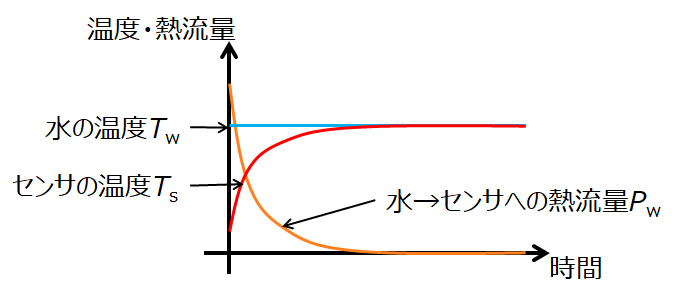

前述の①では一定加熱（Pが定数）であったのに対して、P_wが時間とともに変化するところが温度上昇のメカニズムの大きな違いです。
この場合の時間tのセンサ温度T_s(t)は、式(1) 式(2)の関係から微分方程式として表せます。
熱流量P_w (t)[W]とセンサの熱容量C_s[W/℃]とすると、センサ温度T_s(t)の微分方程式は以下となります。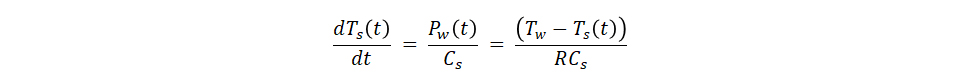
ここでは微分方程式の解法を示しませんが、センサの初期温度T_s0[℃]としたときのセンサ温度T_s(t)について微分方程式を解くと、以下の解が得られます。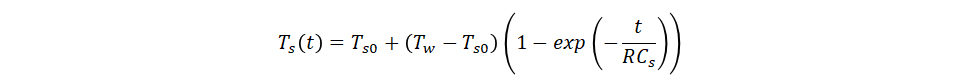

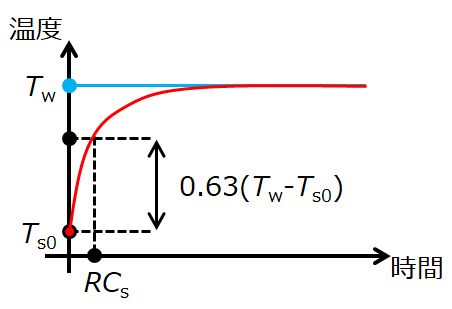
このように、②でのセンサの温度上昇は初期値T_s0、最終値T_w、時定数RC_sとする関数となります。
センサ温度の応答性を決める時定数RC_sには温度が含まれていないため、初期温度、温度の変化量によらず応答時間は一定となることがわかります。
ここで、時定数に含まれるC_sはセンサの熱容量で、センサの材料、形状で決まりますが、Rはセンサと水の間の熱抵抗で、接触条件によっては大きく変化することがあります。
センサの挿入長が十分でなかったり、測定対象との間に隙間ができたりすると熱抵抗が大きくなり、応答特性は悪化します。また、測定対象との間の熱抵抗が大きいと温度を正しく測定することができませんのでご注意ください。

微分方程式導出の補足
式(1)より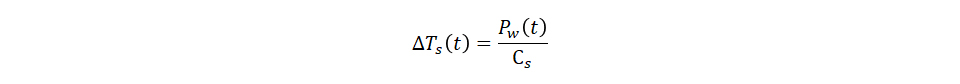

左辺の⊿T_s (t)は時間当たりの温度の変化量のため、センサの温度T_s (t) と⊿t 秒後のセンサ温度T_s (t+⊿t) の変化量は下記のように表せます。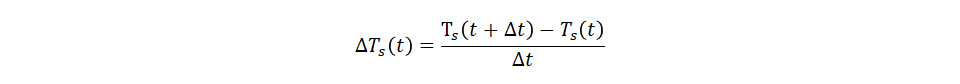この式をはじめの式の⊿T_s (t)に代入し以下の式を得ます。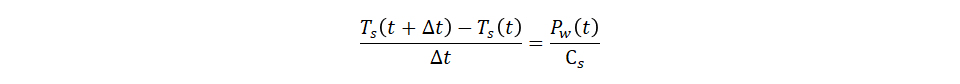またこの時のP_w(t)は式(2)より、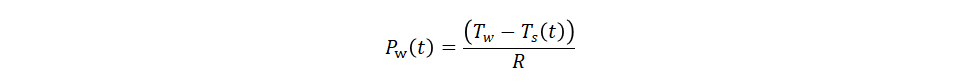これを代入すると、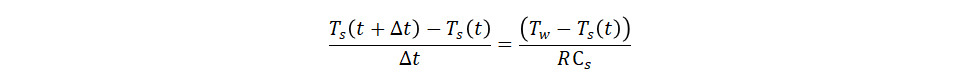これを⊿t→0として微分方程式を得ます。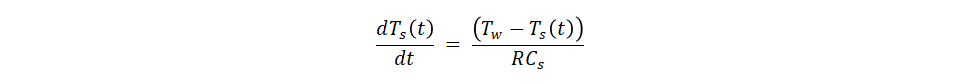

3．まとめ

応答時間が初期温度や温度の変化量によらないことを身近な例と数式を用いて説明しました。
センサを使用するうえでは、測定対象の温度変化と、センサ自身の温度変化の違いを理解することが大切です。